Anyone who has taken Statistics 101 understands the importance of randomness in generating a useful data set, and you don’t need a Ph.D. in game theory to acknowledge the wisdom of conceding a battle or two to win a war.
Putting these basic ideas into practice isn’t always easy.
In my first job out of Wharton, I worked for a consulting firm that had me building statistical models for a major credit card issuer. Our client wanted to know how different customers would respond to changes in the way the bank did business with them, and how that would affect profitability.
So, for example, if they gave someone a credit line increase, our model would look at specific characteristics of that person and predict what would happen in terms of card utilization, likelihood of revolving a balance and likelihood of being delinquent in payment, which would then build up into an overall profitability number.
I won’t pretend the work made my soul “hum,” but it did teach me a few things.
To begin with, there was the bank itself.
In order to build a decent model, we would have needed the credit card issuer to give random credit line increases to thousands of randomly selected cardholders and track the data that interested us. Then we would come back and build our models after a year or two.
Of course, the bank wanted the work done now, and being conservative, they weren’t in the business of extending credit at random either. As a result, we had to work with the data they had, which was biased. Anything we could learn about how people behaved in response to a credit line increase would be limited to those “good” credit risks the bank deemed worthy of receiving additional credit.
That told us nothing about everyone else, despite the fact that people with bad credit might be highly profitable. The bank’s unwillingness to experiment with a tiny group of cardholders and risk a minor blip in their default numbers was leaving a big opportunity on the table.
What does any of this have to do with sports analytics?
Anyone with even a passing interest in professional sports knows winning is paramount. We don’t cheer for our favorite team to lose, and we don’t want coaches and players to throw games (unless a team is so out of playoff contention that we start thinking about next year’s draft.)
But is it always bad to lose?
Put differently, does a team that is so preoccupied with winning display the same sort of conservatism as a bank that leaves money on the table by refusing to extend loans to higher-risk borrowers in exchange for higher yields?
I think so, and here’s why.
At a very general level, the performance of a professional athlete is the product of four elements:
• Ability
• Opportunity
• Quality of opponents
• Randomness
As fans, who have no control over any of these variables, we take all these elements as “given,” but in fact, two of them, opportunity and quality of opponents, are completely determined by coaches and general managers.
For example, those of us who had fantasy football drafts this month pored over rosters trying to find that middling running back with no competition in the backfield and a mediocre quarterback. Such a back might get a lot of “touches” and put up great numbers based on the sheer volume of opportunities available to him (can anyone say Toby Gerhart of the Jacksonville Jaguars?)
Baseball fans know that guys who hit ninth will get fewer plate appearances overall and be less likely to hit with runners on base.
My sport, hockey, is no different. A hockey player’s performance is highly dependent on the quality of his linemates; how much ice time he gets; the situations in which he’s used (for example, does he get power play time); and the opponents he’s thrown out against.
These factors, cast broadly as opportunity and quality of opponents, are predetermined by his coach. We might speculate, but in the absence of actual data, we have no idea what would happen if the player had different opportunities or different opponents.
We must also take into account the possibility that rather than playing the “best” players, coaches may be making on ice decisions that are simply validating the roster choices handed to them by their general managers (presumably with the coach’s input).
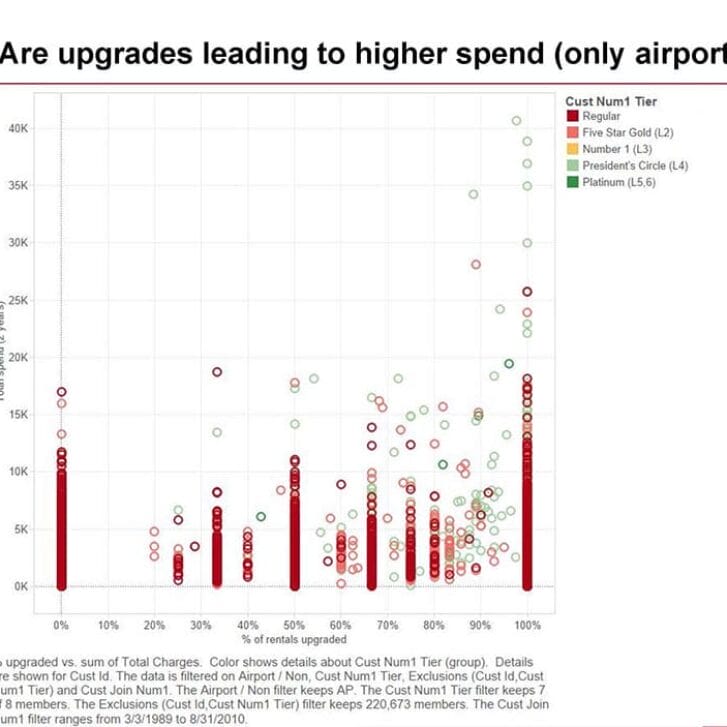
For example, my colleagues and I at the Department of Hockey Analytics recently looked at veteran NHL players last season and found there was a high correlation between what players were paid and their ice time. The correlation between pay and power play ice time, where scoring opportunities are far more frequent, was even higher and not surprisingly, the correlation between power play ice time and power play points was also quite high.
Now unless NHL GMs are complete idiots, one would expect better players to get more ice time, but this phenomenon leaves open the possibility that GMs are “picking their winners” by signing players to big contracts and then protecting their own jobs by ensuring those highly paid players get lots of chances to score and make them look smart.
In other words, equally (or perhaps more) talented players are not getting the same opportunities, or better players are being used in situations where lesser players might do just as well.
Editor’s note: How can hockey and other sports teams—and business organizations—overcome these challenges and embrace unbiased, analytical experimentation? Come back to the Wharton Blog Network next week for the second part of Ian Cooper’s post.